from pylab import *
import time
import scipy.special

%matplotlib inline

plt.rcParams.update({'font.size': 20})
plt.rcParams.update({'text.usetex': True})
matplotlib.rcParams['text.latex.preamble'] = [
    r'\usepackage{amsmath}',
    r'\usepackage{amssymb}']
plt.rcParams.update({'font.family': 'serif', 
                     'font.serif':['Computer Modern']})

def crvec(N, D=1):
    rphase = 2*np.pi * np.random.rand(int(D), int(N))
    return np.cos(rphase) + 1.0j * np.sin(rphase)

def scvec(N, D, K):
    letter_vectors_c = crvec(N, D)

    for d in range(D):
        ip = np.random.choice(int(N), size=int(N-K), replace=False)
        letter_vectors_c[d, ip] = 0
        
    return letter_vectors_c

def lccvec(N, D, K):
    # N needs to be multiple of K
    
    R = N/K
    
    assert(R==N//K)
    
    letter_vectors_c = 0*crvec(N, D)
    
    for d in range(D):
        ip = np.random.choice(int(R), size=int(K), replace=True)
        
        ip += int(R) * np.arange(int(K))
        
        letter_vectors_c[d, ip] = crvec(K, 1)
        
    return letter_vectors_c
    

def cconv(a, b):
    return ifft(fft(a) * fft(b))
    
def ccinv(a):
    return ifft(np.conj(fft(a)))

def lccbind(vec1, vec2, Kv):
    Nv = vec1.shape[0]
    Rv = Nv/Kv

    vec1r = np.reshape(vec1, [int(Kv), int(Rv)])
    vec2r = np.reshape(vec2, [int(Kv), int(Rv)])

    vec_br = cconv(vec1r, vec2r)

    vec_b = vec_br.flatten()
    
    return vec_b

def lccinv(vec1, Kv):
    Nv = vec1.shape[0]
    Rv = Nv/Kv

    vec1r = np.reshape(vec1, [int(Kv), int(Rv)])
    
    vec1_ir = ccinv(vec1r)
    vec1_i = vec1_ir.flatten()
    
    return vec1_i

Sparse binding demo – What’s the dollar of mexico?

To demonstrate the binding operation with sparse block code, we replicate the example from Kanerva’s What we mean when we say ‘What’s the dollar of mexico?’

https://pdfs.semanticscholar.org/f477/232c0a0835dcbc4fc6b6283db484695482f9.pdf

N = 2000
K = 100

# Make a vector for each concept

codebook = lccvec(N, 9, K)
labels = 9*['']

NAM = codebook[0]; labels[0] = 'Name'
CAP = codebook[1]; labels[1] = 'Capitol'
MON = codebook[2]; labels[2] = 'Money'

USA = codebook[3]; labels[3] = 'USA'
WDC = codebook[4]; labels[4] = 'Wash. D.C.'
DOL = codebook[5]; labels[5] = 'Dollar'
MEX = codebook[6]; labels[6] = 'Mexico'
MXC = codebook[7]; labels[7] = 'Mex. City'
PES = codebook[8]; labels[8] = 'Peso'

Now we make a vector that represents the united states and mexico

USTATES = lccbind(NAM, USA, K) + lccbind(CAP, WDC, K) + lccbind(MON, DOL, K)
MEXICO = lccbind(NAM, MEX, K) + lccbind(CAP, MXC, K) + lccbind(MON, PES, K)

# block code vectors are not self-inverses, so we need to do inverse when unbinding
F_UM = lccbind(MEXICO, lccinv(USTATES, K), K)

mex_dol = lccbind(DOL, F_UM, K)

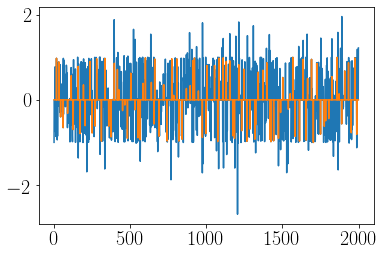
plot(mex_dol)
plot(PES)

/home/epaxon/anaconda3/lib/python3.7/site-packages/numpy/core/numeric.py:538: ComplexWarning: Casting complex values to real discards the imaginary part
  return array(a, dtype, copy=False, order=order)

[<matplotlib.lines.Line2D at 0x7f1db1476e10>]

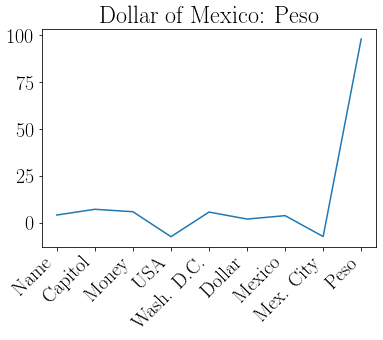
readout = np.real(np.dot(codebook, np.conj(mex_dol)))
plot(readout)
title('Dollar of Mexico: '+ labels[np.argmax(readout)])

ax = gca()
ax.set_xticks(np.arange(len(labels)))
ax.set_xticklabels(labels)
plt.xticks(rotation=45, ha='right')

(array([0, 1, 2, 3, 4, 5, 6, 7, 8]), <a list of 9 Text xticklabel objects>)